Investment time & compound return

In this article you will learn about compound return and find two calculations to back up Selma's focus on investing long-term. It really seems "magic" what compound return can do to your cash once you keep investing long enough.

The magic of compound returns

There is one financial concept that sounds extremely boring but is like a little magic trick that hides in plain sight: Compound interest – and in extension: compound returns.

Compound returns has the biggest impact on growing your money, when you invest as early and for as long as possible. We’re talking about several years – preferably 10, 15 or even more.

The magic basically boils down to one simple idea. That if you hold your money long enough on an investment account (given the right strategy and good care), little by little your returns start to compile returns, without much work from you.

How does compound return work?

"Compound interest (or compounding interest) is interest calculated on the initial principal and which also includes all of the accumulated interest of previous periods of a deposit or loan."
– Investopedia, 2022

Right. Let’s translate that into “human” 😅 An example usually works best. For the sake of a simple demo, all examples below have a fictive av. 6% annual return, the compound return that's paid annually – at the end of the year, and no fees.

Imagine your first investment is 10’000 CHF. Or, in fancier financial terms: "the initial principal".

With our fictive average 6 % market growth, you earn 600 CHF in the first year. At the end of the first year, you will then have 10’600 CHF in total.

That’s easy. What’s next?

In year two, the same fictive 6% return gets you 11’200 CHF. True?

👩🏻‍🔬 Almost. Here’s where things get interesting. Because of the compound “return on return” you got an extra 36 CHF! These come from getting a return on the investment amount you earn after the first year: 6% on 10’600 CHF = 636 CHF.

After year two you now already have 11’236 CHF.

Ten years fly by. With the same example return going strong, you may expect to have 16’000 CHF, correct?

Ah, but now we know about the compound effect! The return-on-return keeps on adding up, and voilà, now you have 1’908 CHF more.

In 10 years, you will then have 17’908 CHF instead of 16’000. Magic! 🔮

Compound return calculated over time

Now, that we know the basic idea behind how compound return works, let’s take a closer look at what kind of impact time has on all of this compounding magic. Our imaginary friends Nora and Harold will help us through it.

Investing for 40 years

Nora starts saving for her retirement. Well, as she calls it – “saving up for the future”, since who thinks about retirement in their 20's? Rock stars? True, but that’s beside the point.

Back to Nora:

🎂 Age 25 years old

⛱ Retirement in 40 years, at 65

🎢 Saving 200 CHF / month

In a friction-free example world, forty years of dedicated, steady savings would bring Nora 96’000 CHF. Not bad, but what about that compound return?

Let’s keep the similar setup as in the previous example.

• A fictive average return of 6% in a year
• No fees or costs
• One yearly compound return payment
• … calculated on that year's average sum

The last point means that the return is based on how much money Nora has on her account at the end of the year – and that number is divided by 12 months.

Here’s Nora’s savings illustrated in a classical financial chart. You might have seen these type of graphs around. This one really got me thinking. Could it really be real? 🤓

Let’s unwrap the graph and the math. After four decades of uninterrupted savings, our devoted saver Nora gets a staggering ~ 289’600 CHF, from the returns alone! That is three times as much she would have saved with simple deposits on her bank account. Well, hello you, compound return. 😏

That’s nearly 382’600 CHF in total. 🔮👩🏻‍🔬

Investing for 30 years

Along comes another imaginary friend, Harold. Thanks to all sorts of targeted, feel-good-intended savings plan ads – mostly featuring handsome senior couples laughing amid picturesque scenery – Harold is getting a constant reminder of the inevitable passage of time. 🙂 Lovely.

Until one day, after years of irregular gigs, Harold lands a stable contract and with smiling grey-haired savings plan ad couple in the back of his head, he decides to get his investments in order.

About Harold

🎂 Age 35 years old

⛱ Retirement in 30 years, at 65

🎢 Saving 200 CHF / month

The previous graph already gave a hint on what happens if the same conditions apply.

After 30 years of stable monthly saving, Harold saves up 72’000 CHF. The return-on-return adds around 123’400 CHF more to the picture. That’s close to 195’400 CHF in total. Not bad. 🔮👩🏻‍🔬

Both, Nora’s and Harold’s, stable monthly investments paid off, the difference that ten years made is pretty mind-blowing. Nora’s approximate 400’000 CHF earnings are nearly double those of Harold’s.

This part still makes me raise my eyebrows and tilt my head a bit while I study the graph. Huh? This is where compound returns really hit the home run.

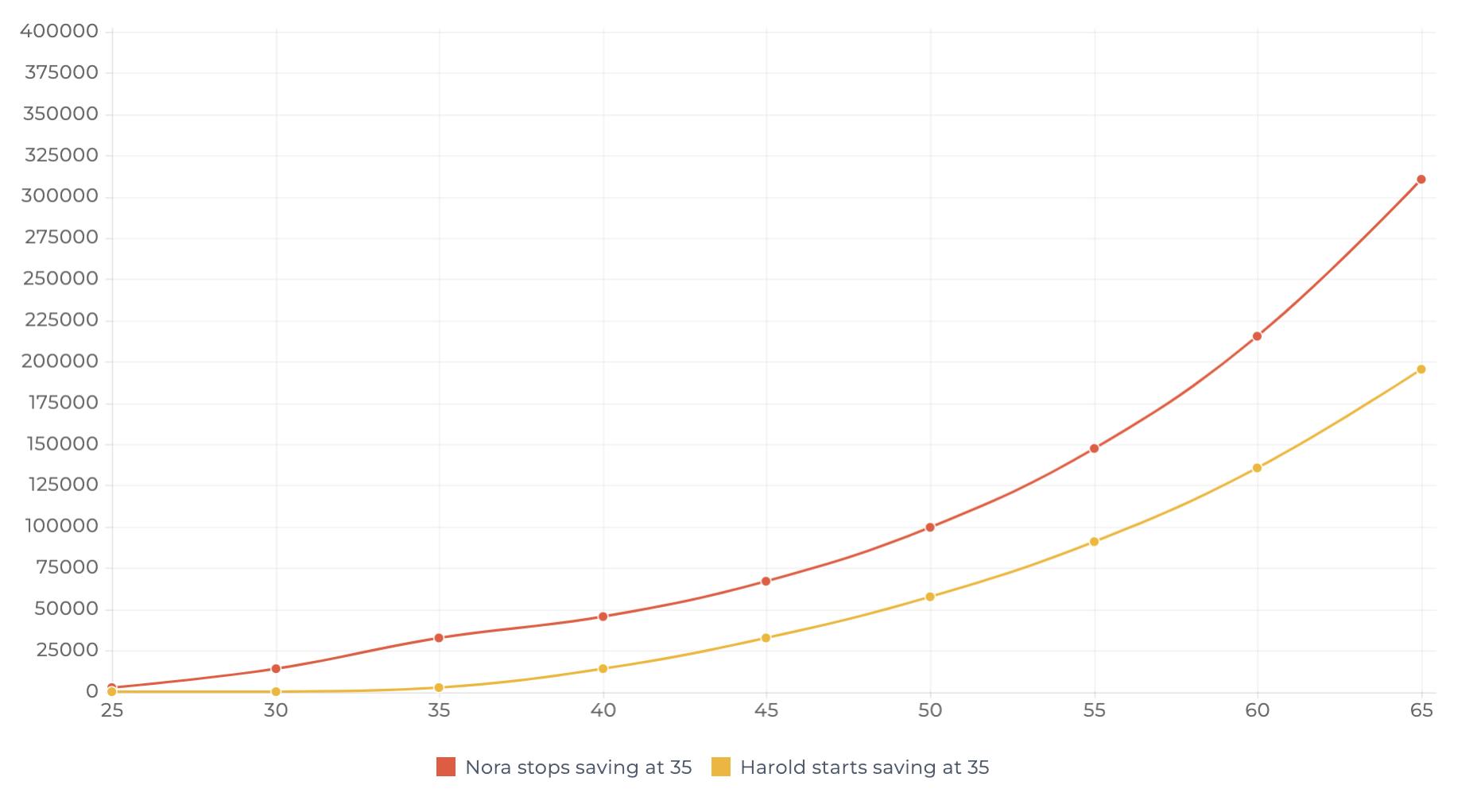
🤓 Imagine that after ten years, Nora would have stopped saving monthly. How would that compare to Harold’s non-stop investing? Surely Harold’s investments would catch up with Nora’s then?

🧐 Oddly enough, even though Nora stopped investing more money when she was 35 years old - at Harold’s age of starting to invest - his investments did not catch up.

Nora invested 24’000 CHF in total, Harold invested 60’000 CHF. Add time into the equation (40 years in this case!) and this is what you get.

Extra tip for when you’re doubtful after a short period of time:

The trick lies in “sticking with it”. After five years, the compound returns don't look like too much – am I right?

It kind of feels like, nothing is happening, which is why we are calling compound return this “magical thing hiding in plain sight”. It’s there and working, but you don’t see it for a couple of years. After ten or twenty years, the relation between what you had in the beginning and the compounded earnings is staggering.